La fonction exponentielle

C’est le mathématicien suisse Leonhard Euler (1707-1783) utilisa pour la première fois la notation e. La première apparition de la lettre « e » pour désigner la base du logarithme népérien date de 1728, dans un manuscrit d’Euler qui le définit comme le nombre dont le logarithme est l’unité et qui se sert des tables de Vlacq pour l’évaluer à 2,7182817.

La forme prise par un fil pesant flexible entre deux point fixe est appelée une “chaînette”
C’est une courbe de fonction qui fait intervenir la fonction exponentielle !

1. Définition de la fonction exponentielle

1.1 Définition

Approche

On cherche à résoudre une équation différentielle, c’est à dire une équation qui met en relation une fonction avec sa dérivée.
On va s’intéresser ici à la (il y en a qu’une seule) fonction (elle existe) telle que :

• Pour tout réel $x \in \mathbb{R}$, $f(x)=f'(x)$
• $f(0)=1$

Propriété 1

Il existe une et une seule fonction $f$ dérivable sur $\mathbb{R}$ telle que :

• $f(0)=1$
• $f'=f$

Définition 1

Cette fonction est appelée fonction exponentielle et est notée $exp$.\
Ainsi, pour tout $x \in \mathbb{R}$, on a :

• $exp(0)=1$
• $exp'(x)=exp(x)$

1.2 Propriétés

Propriété 2

Pour tout réel $x$, on a $exp(-x)\times exp(x)=1$

Exemple 1

• $exp(5)=$
• $exp(-8)=$

Conséquences

Pour tout $x \in \mathbb{R}$, $exp(x) \neq 0$

1.3 Propriétés algébriques

Propriété 3

Pour tous réels $x$ et $y$, et pour tout entier relatif $n$, on a :

• $exp(-x)=\dfrac{1}{exp(x)}$
• $exp(x+y)=exp(x)\times exp(y)$
• $exp(x-y)=\dfrac{exp(x)}{exp(y)}$
• $exp(nx)=(exp(x))^n$

Exemple 2

• $exp(-5)=$
• $exp(8)=exp(5+3) =$
• $exp(4)=exp(6-2) =$
• $exp(40)=exp(4\times 10) =$

SF1: Savoir manipuler les propriétés algébriques

• Soit $x$ un réel. Simplifier les expressions suivantes:
  • $A = exp(4x)\times exp(-2x+1)$
  • $B=\dfrac{(exp(x+1))^2}{exp(3x-4)}$
• Montrer que pour tout réel $x$, on a :
  $\dfrac{1-exp(-x)}{1+exp(-x)}=\dfrac{exp(x)-1}{exp(x)+1}$

2. Une nouvelle notation !

Les propriétés algébriques vues précédemment nous permettent de constater que les formules sont analogues aux règles de calcul sur les puissances.
On introduit donc une nouvelle notation : $exp(x)=e^x$

2.1 Le nombre $e$

Avec la nouvelle notation, on a donc $exp(1)=e^1=e$.

Définition 2

L’image de 1 par la fonction exponentielle est notée $e$.

2.2 Les propriétés algébriques

Propriété 4

Pour tous réels $x$ et $y$, et pour tout entier relatif $n$, on a :

• $e^{-x}=\dfrac{1}{e^{x}}$
• $e^{x+y}=e^{x}\times e^{y}$
• $e^{x-y}=\dfrac{e^{x}}{e^{y}}$
• $e^{nx}=\left(e^{x}\right)^n$

2.3 Lien avec les suites géométriques

Approche

Imaginons une quantité qui vaut 1 initialement et qui double chaque heure
On a donc $u_0=1$, $u_1=2$, $u_2=4$ …
La suite $(u_n)$ est géométrique, par construction.

• Donner la formule explicite de la suite $(u_n)$.
• Déterminer à tâtons, et le plus précisément possible la valeur approchée de $a$ tel que $e^a=2$

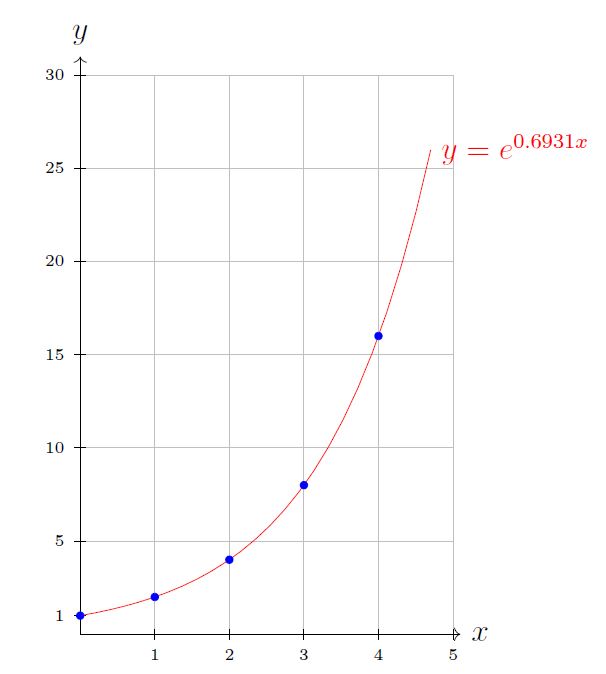
Il est donc maintenant possible d’avoir une estimation de la quantité au bout de 2.5 heures, ce qui n’était pas possible avec les suites !

Ce passage du “discret” au “continu” grâce à la fonction exponentielle permet de modéliser de nombreuses évolutions dans des domaines variés, comme le calcul d’intérêts, la dilution d’une solution, la décroissance radioactive…etc…

Propriété 5

Pour tout réel $a$, la suite $(u_n)$ définie par $u_n=e^{na}$ est une suite géométrique.

Exemple 2

la suite $(u_n)$ définie pour tout $n \in \mathbb{N}$ par $u_n=e^{2n}$ est une suite géométrique.

• $u_1=$
• $u_2=$
• $u_3=$

Démonstration 1

Soit $a$ un réel. Montrer que la suite $(u_n)$ définie pour tout $n \in \mathbb{N}$ par $u_n=e^{an}$ est une suite géométrique dont on précisera la raison.

3. Étude de la fonction exponentielle

3.1 Signe de la fonction exponentielle

Propriété 6

La fonction exponentielle est strictement positive sur $\mathbb{R}$.
Ainsi, pour tout réel $x \in \mathbb{R}$, on a $e^x>0$

Démonstration 3

Montrer que pour tout réel $x \in \mathbb{R}$, on a $e^x>0$.

3.2 Sens de variation de la fonction exponentielle

Sens de variations

Propriété 7

La fonction exponentielle est strictement croissante sur $\mathbb{R}$.

<<<<<<< HEAD

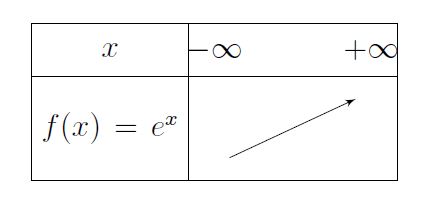
Démonstration 4

=======

Démonstration

>>>>>>> c19e6991be414f88121a553cebd7afd2af6db2f8

Montrer que la fonction exponentielle est strictement croissante sur $\mathbb{R}$.

Remarque

La fonction exponentielle est de croissance très rapide, d’où l’expression courante de “croissance exponentielle”.

SF2 : Savoir résoudre des équations et inéquations avec la fonction exponentielle

Résoudre dans $\mathbb{R}$

1. $e^{3x}=e^{5x+2}$
2. $e^{x+1}>e^{5x}$
3. $e^{7x-1}\leq e^{x}$
4. 4.$e^{x+1}=1$
5. $e^x>1$
6. $e^{x+3}<0$
7. $-2e^{x+2} \geq -2e^{-5}$
8. $e^{-x}-e \leq 0$

3.3 Représentation graphique

Tableau de valeurs :

$x$	-4	-3	-2	-1	0	1	2	3	4
$f(x)$	0.02	0.05	0.14	0.37	1	2.72	7.39	20.09	54.60

Courbe représentative de la fonction exponentielle :

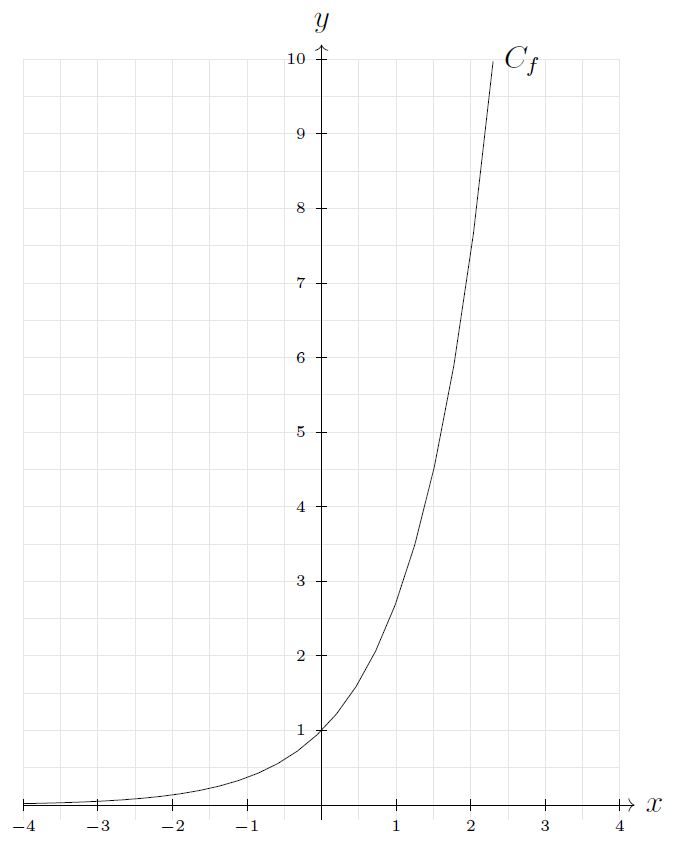
Remarque

• La courbe $C_f$ passe par les points de coordonnées $(0,1)$ et $(1,e)$.
• La courbe $C_f$ est situé au dessus de l’axe des abscisses, et ne le coupe jamais.

3.4 Dérivée de la fonction $g$ définie par $g(x)=exp(ax+b)$

Propriété 8

Soient $a$ et $b$ deux réels.
La fonction $f$ définie sur $\mathbb{R}$ par $f(x)=e^{ax+b}$ est dérivable sur $\mathbb{R}$, et pour tout réel $x\in\mathbb{R}$, on a $f'(x)=a\times e^{ax+b}$.

Exemple 3

Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=e^{2x+1}$.
Calculer $f'(x)$

SF3: Savoir étudier une fonction comportant une exponentielle

1. Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=e^{2x}-2x$.
   1. Calculer $f'(x)$
   2. Etudier les variations de la fonction $f$.
   3. En déduire le signe de $f$ sur $\mathbb{R}$.
   4. Déterminer une équation de la tangente $\mathscr{D}$ à $C_f$ passant par le point de la courbe d’abscisse $\frac{1}{2}$.
   5. La droite $\mathscr{D}$ passe-t-elle par l’origine du repère ?
   6. Vérifier les résultats précédents à l’aide de la calculatrice.
2. Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=\dfrac{1}{1+e^x}$.
   1. Calculer $f'(x)$
   2. Étudier les variations de la fonction $f$.
   3. Déterminer une équation de la tangente $\mathscr{D}$ à $C_f$ passant par le point de la courbe d’abscisse $0$.
   4. Vérifier les résultats précédents à l’aide de la calculatrice.
3. Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=(x+1)e^x$.
   1. Étudier les variations de la fonction $f$.
   2. Vérifier les résultats précédents à l’aide de la calculatrice.

3.5 Fonction $e^{kx}$, où $k\in\mathbb{R}$

• si $k>0$, la fonction $f$ définie par $f(x)=e^{kx}$ est strictement croissante sur $\mathbb{R}$
• si $k<0$, la fonction $f$ définie par $f(x)=e^{kx}$ est strictement décroissante sur $\mathbb{R}$

Voir l’animation géogébra qui trace la courbe de la fonction $f(x)=e^{kx}$ en fonction des valeurs de $k$.